
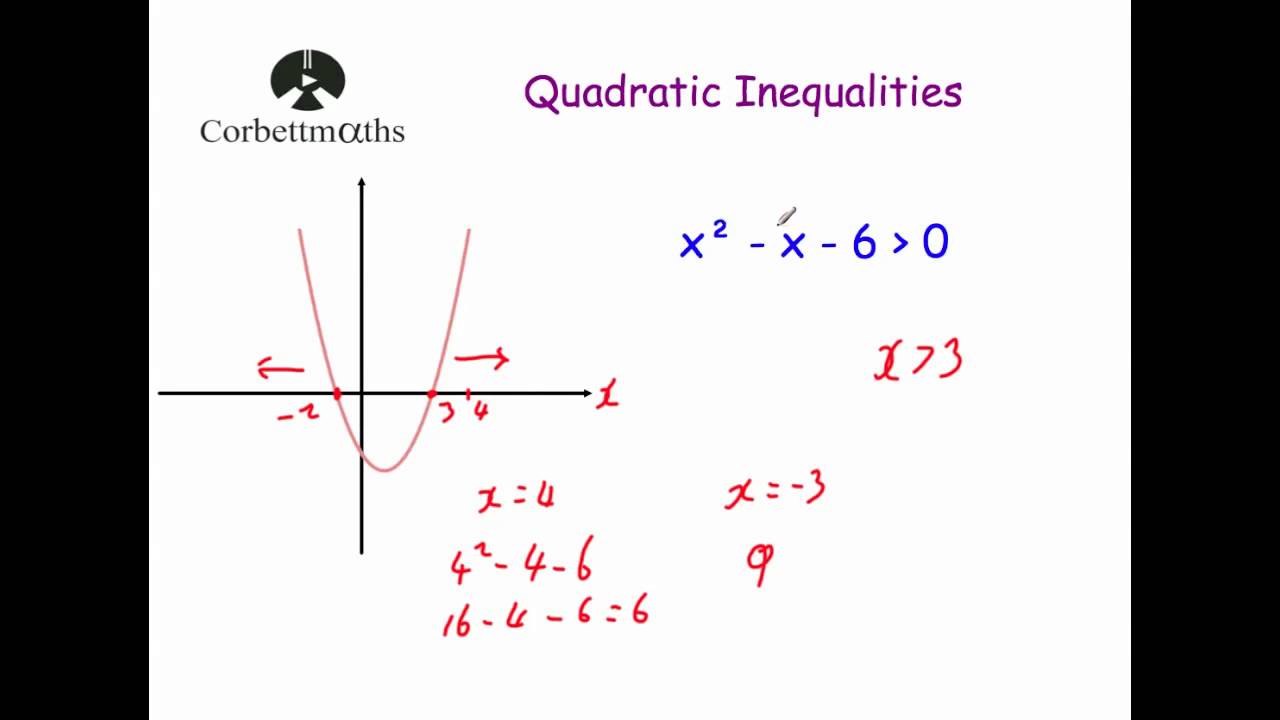
This page titled 9.9: Solve Quadratic Inequalities is shared under a CC BY 4.0 license and was authored, remixed, and/or curated by OpenStax via source content that was edited to the style and standards of the LibreTexts platform a detailed edit history is available. We are only concerned if the function is positive or negative and thus a complete calculation is not necessary. A quadratic inequality is an inequality that contains a quadratic expression. To make a sign chart, use the function and test values in each region bounded by the roots.Therefore, set the function equal to zero and solve. For a quadratic inequality in standard form, the critical numbers are the roots.

Shade in the appropriate x-values depending on the original inequality. It is important to note that this quadratic inequality is in standard form, with zero on one side of the inequality. A sign chart gives us a visual reference that indicates where the function is above the x-axis using positive signs or below the x-axis using negative signs. We can streamline the process of solving quadratic inequalities by making use of a sign chart.If the inequality involves “greater than,” then determine the x-values where the function is above the x-axis. The above is an equation () but sometimes we need to solve inequalities like. If the inequality involves “less than,” then determine the x-values where the function is below the x-axis. Graph the quadratic function and determine where it is above or below the x-axis. A quadratic inequality is of the form: a x 2 + b x + c > 0 Where a 0, and our > can be replaced with any inequality symbol. What happens as you change the value of 'a' By using the check boxes look at what is happening with the regions. Use the Geogebra file to investigate the nature of quadratic inequalities. We can solve quadratic inequalities graphically by first rewriting the inequality in standard form, with zero on one side. Investigating Regions of Quadratic Inequalities.inequality, we seek the range xthat satisfy.
If we solve the quadraticinequality, the number of solutions is infinite, but, they will lie within a given range. This quadratic equation has two unique or distinct roots.
#QUADRATIC INEQUALITIES HOW TO#
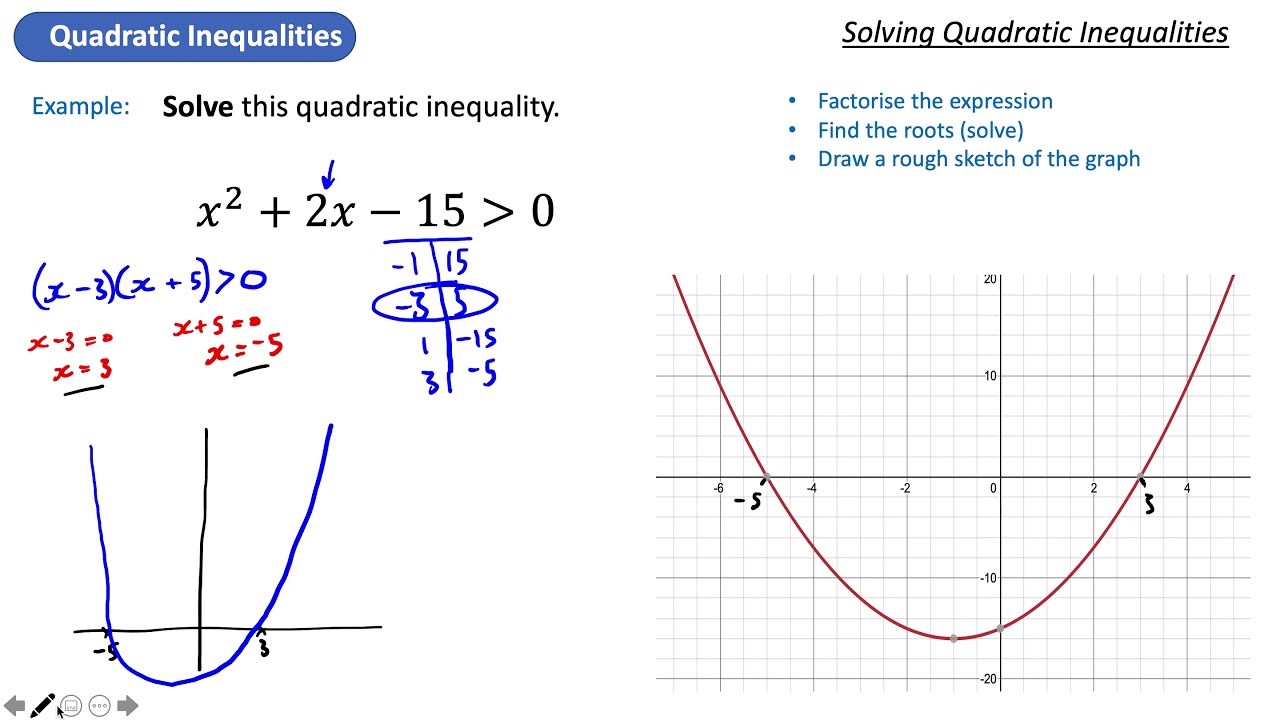
Quadratic Formulas are Addressed by Factorization TechniqueĬonsidering that we understand quadratic inequalities can be fixed comparably as square formulas. Example 9.9.1: How to Solve a Quadratic Inequality Graphically. Remember that there are four different methods for solving a quadratic.
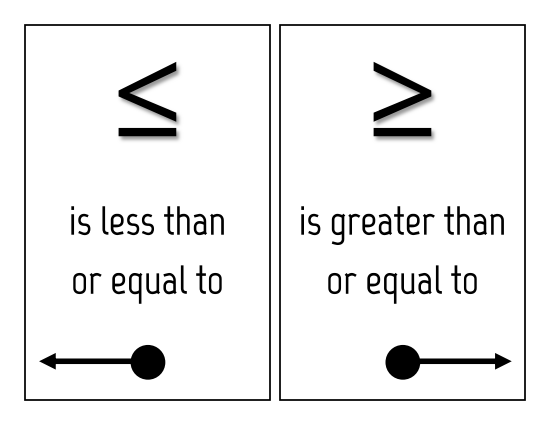
Before we can learn how to resolve Quadratic inequalities, let’s remember just how to square equations are solved by managing a few instances. To solve a quadratic inequality, we first find the x x -intercepts of the graph. Quadratic formulas can be resolved by either the factorization approach or by utilize of the square formula. Those solutions are called the critical numbers of the. Yet, with inequalities, you want to know either side of the no, i.e. Pretend the inequality symbol is an equal sign and solve the corresponding quadratic equation. The only exemption is that, with quadratic equations, you correspond the expressions to no. Before we get to quadratic inequalities, lets just start graphing some functions and interpret them and then well slowly move to the inequalities. Instances of quadratic inequalities are: x2– 6x– 16 ≤ 0, 2×2– 11x + 12 > 0, x2 + 4 > 0, x2– 3x + 2 ≤ 0 etcĪddressing a quadratic inequality in Algebra resembles managing a quadratic equation. Welcome to the presentation on quadratic inequalities. Find all a so that the following equation would have a possitive solution: Solution: 5. Let us consider the quadratic inequality x2 5x <.
X2– 6x– 16 ≤ 0, 2×2– 11x + 12 > 0, x2 + 4 > 0, x2– 3x + 2 ≤ 0 and so on Solving Quadratic InequalitiesĪ quadratic inequality equation of a second degree uses an inequality indicator instead of an equal sign. The standard quadratic equation becomes an inequality if it is represented as ax2 + bx + c < 0 or (>0).Hence, ax2 + bx + c ≥ 0 Examples of Quadratic inequalities are:


 0 kommentar(er)
0 kommentar(er)
